https://www.acmicpc.net/problem/1520
- 예제 입력
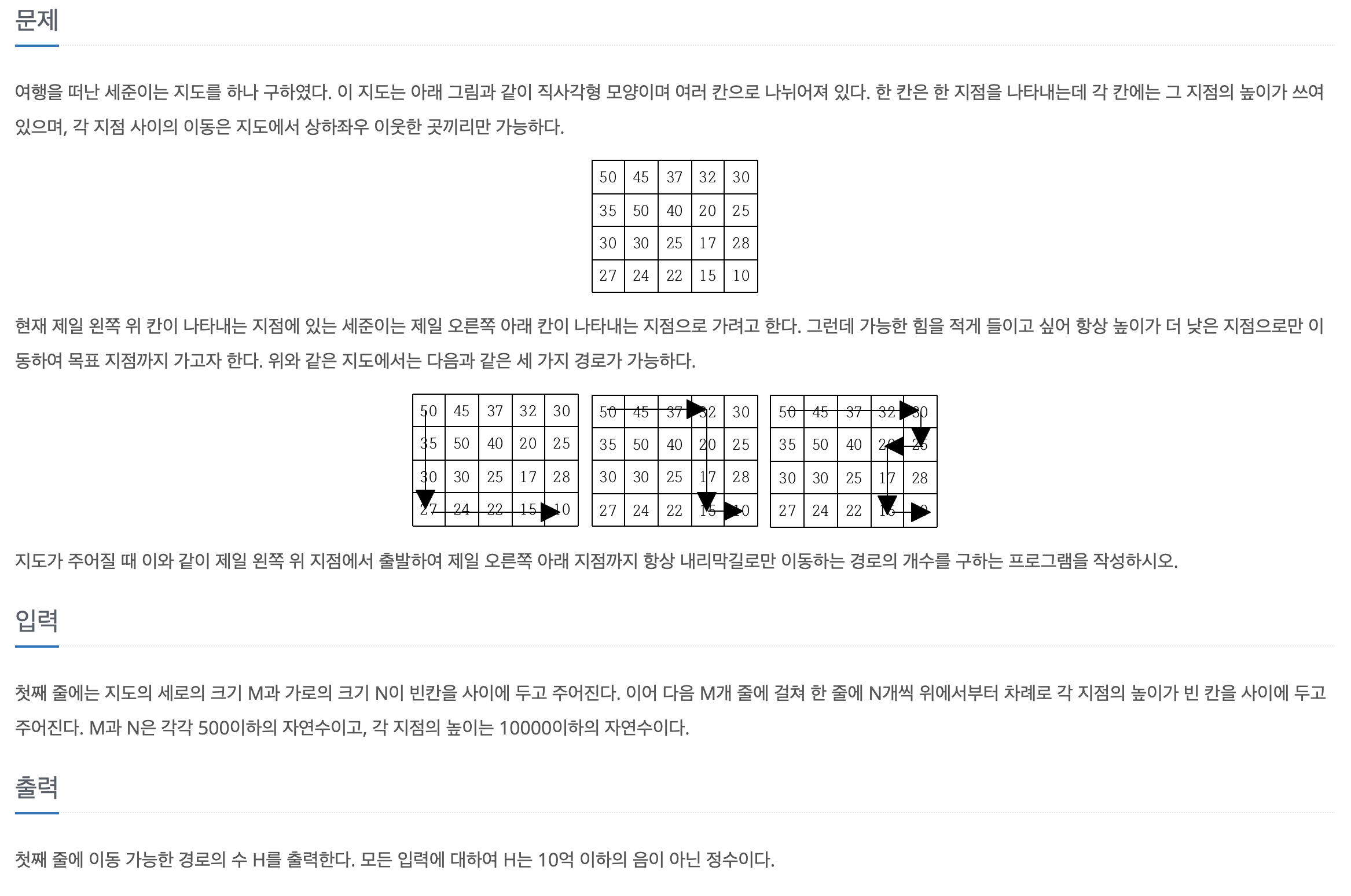
4 5
50 45 37 32 30
35 50 40 20 25
30 30 25 17 28
27 24 22 15 10
- 예제 출력
3
풀이
처음에 단순히 BFS로 풀었는데 메모리 초과로 실패했다.
때문에 메모이제이션을 사용하는 방법으로 한다.
위 예제 입출력으로 답이 3이다.

이 사진처럼 (0,3)위치에서 목적지(최 우측 하단)로 가는
방법은 2가지가 나온다. 그렇다면 n*m 크기의 dp배열에
해당 경로에서 목적지까지 가는 경로의 경우의 수를 메모이제이션 해서 쓰는
방식으로 한다면 복잡도를 크게 줄일 수 있다.
또한 탐색은 dfs 재귀를 이용한다.
dp배열은 -1 값으로 초기화 한다.
dp[?][?] == -1 => 탐색
dp[?][?] != -1 => 이미 탐색했으므로 dp[?][?]를 리턴!
전체코드
import java.util.*;
class Main {
static int[] dy = {-1,0,1,0};
static int[] dx = {0,1,0,-1};
static int[][] arr;
static int[][] dp;
static int n,m;
public static int dfs(int y, int x){
// 목적지 도착 시 왔던 경로들을 1씩 더해줌
if(y==n-1 && x==m-1) return 1;
// 이미 계산 끝난 경로는 메모이제이션
if(dp[y][x] != -1) {
return dp[y][x];
}
// 탐색
else{
dp[y][x] = 0;
for(int i=0; i<4; i++){
int ny = y+ dy[i];
int nx = x+ dx[i];
if(ny<0 || ny>=n || nx<0 || nx>=m) continue;
// 다음 경로가 더 낮을때만
if(arr[y][x] > arr[ny][nx]) {
dp[y][x] += dfs(ny,nx); // 다음 경로 누적 없으면 0이 누적될거임
}
}
return dp[y][x];
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//input
n = sc.nextInt();
m = sc.nextInt();
arr = new int[n][m];
dp = new int[n][m];
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
arr[i][j] = sc.nextInt();
dp[i][j]=-1;
}
}
//solve
int answer = dfs(0,0);
//output
System.out.println(answer);
}
}
결과를 보면 왼쪽이
4*5 크기의 arr배열이고 오른쪽이 dp배열이다 시작점(0,0) 에서 경로의 경우의 수가
잘 누적되어 3이 나온것을 볼 수 있다.


'알고리즘 > 문제풀이' 카테고리의 다른 글
| 백준 0 만들기 - Java (0) | 2024.07.02 |
|---|---|
| 백준 1776 문제집 - Java (0) | 2024.06.25 |
| 백준 11497 통나무 건너뛰기 - Java (0) | 2024.06.14 |
| 백준 14503 로봇 청소기(시뮬레이션) - Java (1) | 2024.06.13 |
| 백준 1823 수확(DP) - Java (1) | 2024.06.10 |



